$$ \sim * \backsim $$
Table of Contents
$$ \backsim * \sim $$
In the last chapter, we studied the quantum teleportation protocol, which transmitted one qubit using two classical bits of communication, at the cost of one entangled e-bit.
The superdense coding protocol achieves the exact inverse. It allows for the transmission of two classical bits using on qubit of quantum information, at the cost of one e-bit.
Of course, there are much simpler ways of achieving classical bit transmission. Nevertheless it is still important as it demonstrates another evident use of entanglement.
§ 13. Superdense Coding Protocol
The following quantum circuit defines the superdense coding protocol:
 Figure 11: Superdense Coding Protocol
Figure 11: Superdense Coding Protocol
Retrieved from IBM Quantum Learning
$d$ and $c$ are the two classical bits of information we wish to transmit. Together, Alice’s qubit $A$ and Bob’s qubit $B$ are in the entangled Bell state $|\phi^+\rangle$.
Here is what Alice does:
- if $d = 0$, Alice performs the Identity gate on her qubit $A$.
- if $c = 0$, Alice performs the Identity gate on her qubit $A$.
$\backsim$ * $\sim$
- if $d = 1$, Alice performs a $Z$ gate on her qubit $A$.
- if $c = 1$, Alice performs an $X$ gate on her qubit $A$.
Alice afterwards sends qubit $A$ to Bob.
When Bob receives qubit $A$
- He applies a CNOT gate, with $A$ as the control and $B$ as the target.
- He applies a Hadamard Gate to $A$.
- He measures $B$ to obtain $c$ and measures $A$ to obtain $d$.
Analysis
The idea behind this protocol is fairly simple. By implementing $Z$ and $X$ gates depending on the values of $c$ and $d$, Alice effectively chooses which Bell State she shares with Bob.
Alice and Bob initially share $|\phi^+\rangle$. Depending on the values of $c$ and $d$, Alice performs the following actions:
$$ \begin{align} cd &= 00: \qquad (\mathbb{1} \otimes \mathbb{1})|\phi^+\rangle &= |\phi^+\rangle \\ cd &= 01: \qquad (\mathbb{1} \otimes Z)|\phi^+\rangle &= |\phi^-\rangle \\ cd &= 10: \qquad (\mathbb{1} \otimes X)|\phi^+\rangle &= |\psi^+\rangle \\ cd &= 11: \qquad (\mathbb{1} \otimes XZ)|\phi^+\rangle &= |\psi^-\rangle \\ \end{align} $$
Bob’s actions then have the following effects on the four Bell states:
$$ \begin{align} |\phi^+\rangle &\rightarrow &|00\rangle \\ |\phi^-\rangle &\rightarrow &|01\rangle \\ |\psi^+\rangle &\rightarrow &|10\rangle \\ |\psi^-\rangle &\rightarrow &-|11\rangle \\ \end{align} $$
which after a measurement gate, becomes $cd$.
§ 14. Qiskit Implementation
# Required imports
from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister
from qiskit_aer.primitives import Sampler
from qiskit_aer import AerSimulator
from qiskit.visualization import plot_histogram
Let’s first specify the bits we wish to be transmitted.
# Setting bits we wish to transmit
c = "1"
d = "0"
Now we’ll build the circuit accordingly. First try building the circuit yourself!
protocol = QuantumCircuit(2)
# Prepare ebit |ϕ+> used for superdense coding via Bell Circuit
protocol.h(0)
protocol.cx(0, 1)
protocol.barrier()
# Alice's operations
if d == "1":
protocol.z(0)
if c == "1":
protocol.x(0)
protocol.barrier()
# Bob's operations
protocol.cx(0, 1)
protocol.h(0)
protocol.measure_all()
display(protocol.draw())
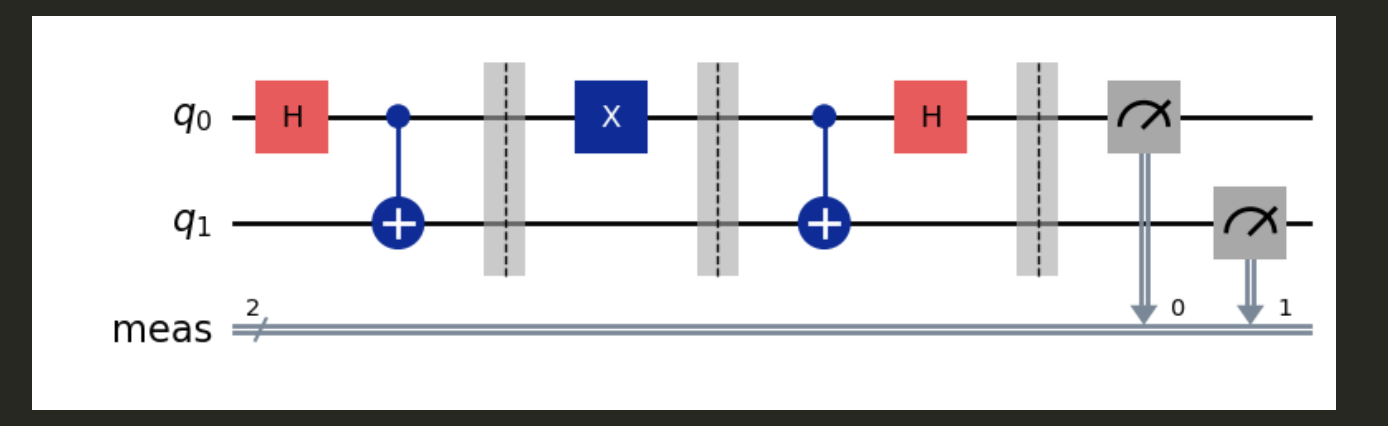
Rather than placing the measurements into separate classical bits, we use the measure_all() method.
The measure_all() method measures all of the qubits and places the results in a single classical register.
Let’s run the AerSimulator() and see the result.
job = AerSimulator().run(protocol)
result = job.result()
statistics = result.get_counts()
plot_histogram(statistics)

As expected, $cd = 10$.
Exercises
This chapter only has one exercise.
- Devise a way to evenly randomize the values of $c$ and $d$ into 00, 01, 10, and 11 using a qubit. Afterwards implement the superdense coding protocol and show Alice’s and Bob’s values of $c$ and $d$ always agree.
Hint: Use the Hadamard Gate
$\hspace{1px}$
$\hspace{1px}$
$\hspace{1px}$
$\hspace{1px}$
$\hspace{1px}$
$\hspace{1px}$
Solutions
We use the Hadamard Gate, which has the following effect on $|0\rangle$ and $|1\rangle$:
$$ \begin{align} \hat{H}|0\rangle &= \frac{1}{\sqrt{2}}|0\rangle + \frac{1}{\sqrt{2}}|1\rangle \equiv |+\rangle \\ \hat{H}|1\rangle &= \frac{1}{\sqrt{2}}|0\rangle - \frac{1}{\sqrt{2}}|1\rangle \equiv |-\rangle. \end{align} $$
Performing a measurement gate on $|+\rangle$ or $|-\rangle$ yields a 0 or 1 with an equal 1/2 probability, acting as a randomizer. The measurement gate also converts $|+\rangle$ and $|-\rangle$ back into $|0\rangle$ and $|1\rangle$, respectively.
We perform the above Hadamard + Measurement operation for both c and d.
Here is the circuit:
rbg = QuantumRegister(1, "randomizer")
ebit0 = QuantumRegister(1, "A")
ebit1 = QuantumRegister(1, "B")
Alice_c = ClassicalRegister(1, "Alice c")
Alice_d = ClassicalRegister(1, "Alice d")
test = QuantumCircuit(rbg, ebit0, ebit1, Alice_d, Alice_c)
# Initialize the ebit
test.h(ebit0)
test.cx(ebit0, ebit1)
test.barrier()
# Use the 'randomizer' qubit twice to generate Alice's bits c and d.
test.h(rbg) # |0> -> |+>
test.measure(rbg, Alice_c) # Produces |0> or |1> with 1/2 probability
# Places result into `c`
test.h(rbg)
test.measure(rbg, Alice_d) # Produces |0> or |1> with 1/2 probability
# Places result into `d`
test.barrier()
# Now the protocol runs, starting with Alice's actions, which depend
# on her bits.
with test.if_test((Alice_d, 1), label="Z"):
test.z(ebit0)
with test.if_test((Alice_c, 1), label="X"):
test.x(ebit0)
test.barrier()
# Bob's actions
test.cx(ebit0, ebit1)
test.h(ebit0)
test.barrier()
Bob_c = ClassicalRegister(1, "Bob c")
Bob_d = ClassicalRegister(1, "Bob d")
test.add_register(Bob_d)
test.add_register(Bob_c)
test.measure(ebit0, Bob_d)
test.measure(ebit1, Bob_c)
display(test.draw('mpl'))
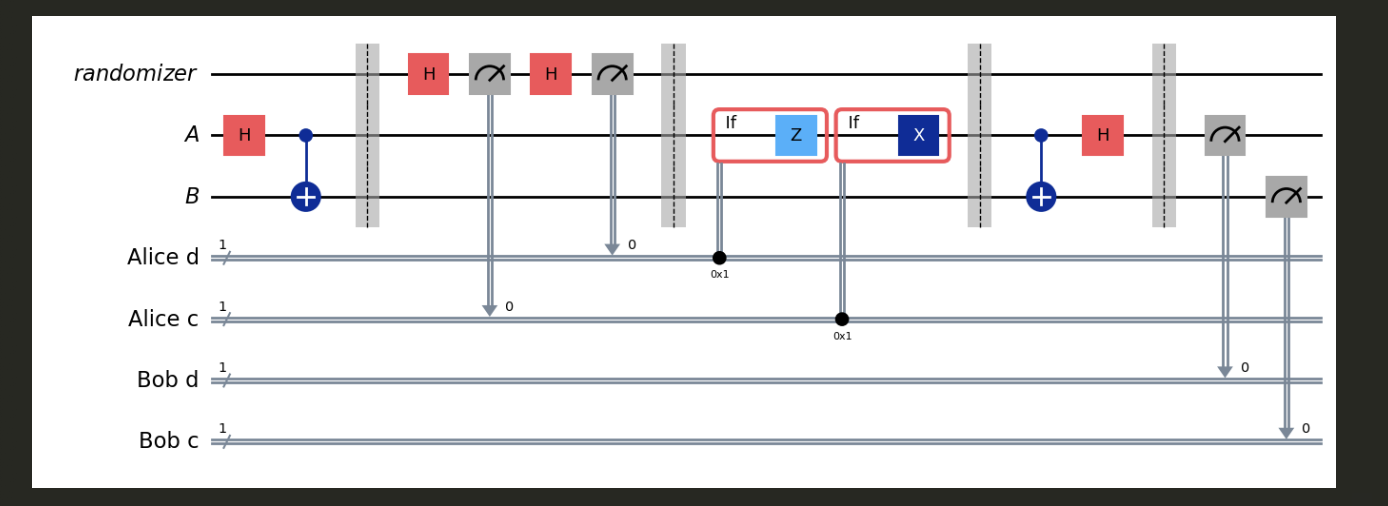
Running the AerSimulator():
job = AerSimulator().run(test, shots = 1000)
result = job.result()
statistics = result.get_counts()
display(plot_histogram(statistics))
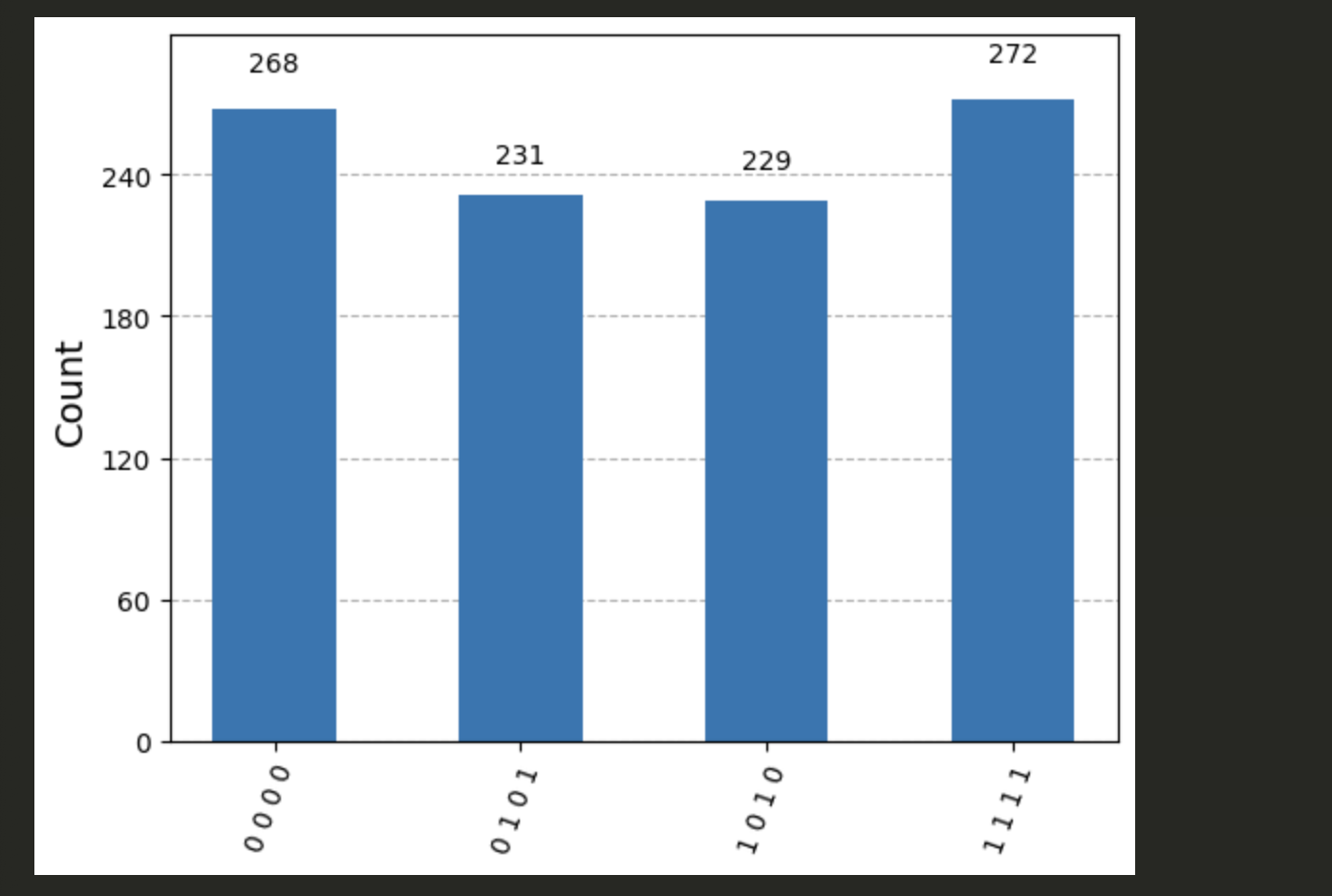
Alice and Bob’s classical bits always agree.
Previous – Quantum Teleportation $\sim$*$\backsim$ Next – The CHSH Game